Diketahui titik $A, B$, dan $C$ pada bidang Kartesius seperti gambar berikut.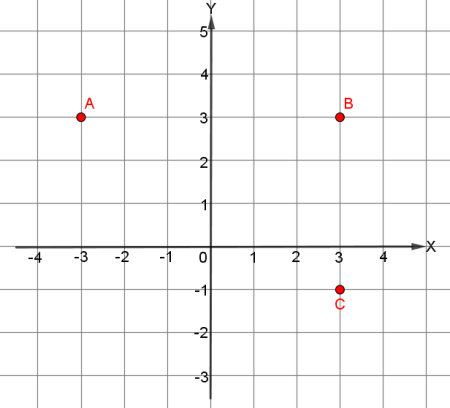
- Tentukan koordinat titik $D$ agar terbentuk persegi panjang $ABCD$.
- Tentukan keliling persegi panjang $ABCD$.
- Tentukan luas persegi panjang $ABCD$.
- Tentukan panjang diagonal $BD$.
Dari gambar, diketahui koordinat titik $A$ adalah $(-3, 3)$, $B(3, 3)$, dan $C(3, -1)$.
Jawaban a)
Agar terbentuk persegi panjang $ABCD$, maka $D$ harus terletak di sekitar kuadran III, tepatnya di titik $(-3, -1)$, seperti yang tampak pada gambar berikut.
Jawaban b)
Keliling bangun datar adalah jumlah panjang setiap sisi-sisinya. Oleh karena itu,
$$\begin{aligned} \text{k}_{ABCD} & = AB + BC + CD + AD \\ & = 6 + 4 + 6 + 4 \\ & = 20 \end{aligned}$$Jadi, keliling persegi panjang $ABCD$ adalah $\boxed{20}$ satuan panjang.
Jawaban c)
Luas persegi panjang sama dengan panjang dikali lebarnya. Oleh karena itu,
$$\begin{aligned} \text{L}_{ABCD} & = AB \times BC \\ & = 6 \times 4 \\ & = 24 \end{aligned}$$Jadi, luas persegi panjang $ABCD$ adalah $\boxed{24}$ satuan luas.
Jawaban d)
Untuk menentukan panjang diagonal $BD$, gunakan rumus Pythagoras di segitiga siku-siku $BCD$.
$$\begin{aligned} BD & = \sqrt{BC^2 + CD^2} \\ & = \sqrt{4^2 + 6^2} \\ & = \sqrt{16 + 36} \\ & = \sqrt{52} = \sqrt{4 \times 13} = 2\sqrt{13} \end{aligned}$$Jadi, panjang diagonal $BD$ adalah $\boxed{2\sqrt{13}}$ satuan panjang.
Semoga pembahasan soal Koordinat Menentukan Luas Sebuah Bangun ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.
Cari Soal dan Pembahasan tentang alat optik, koordinat