Topik Bahasan
turunan
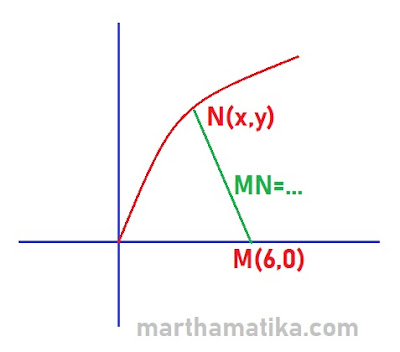
Jarak terdekat titik (6,0) ke kurva y=2$\sqrt x$ adalah...
Pembahasan:
Untuk materi dan rumus silakan baca: Cara Menghitung Jarak terdekat titik pada Kurva grafik
Misalkan:
M= (a,b)= (6,0)
Asumsikan ada satu titik pada kurva /grafik y=2$\sqrt x$ yakni (x,y).
$ MN= \sqrt {(x-a)^2 + (y-b)^2} \\ MN= \sqrt {(x-6)^2 + (y-0)^2}$
Subtitusikan y=2$\sqrt x$
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2} \\ MN = \sqrt { x^2-12x+36 +4x} \\ MN = ( x^2-12x+36 +4x)^ {\frac {1}{2}}$
Sesuai syarat maksimum dan minimum dimana terjadi saat turunan pertama =0 maka,
$ \frac {d(MN}{dx}=0 \\ \frac {2x-12+4}{ \sqrt { x^2-12x+36 +4x} } =0 \\ 2x-8 =0 \\ x=4$
Jadi jarak terdekat itu terjadi saat x=4. Silakan disubtitusi ke persamaan:
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2}\\ MN =\sqrt {(4-6)^2 + (2\sqrt 4-0)^2} = 2 \sqrt 5$.
Semoga pembahasan soal Contoh Soal Jarak Terdekat Titik ke Kurva dengan Turunan ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.
Jarak terdekat titik (6,0) ke kurva y=2$\sqrt x$ adalah...
Pembahasan:
Untuk materi dan rumus silakan baca: Cara Menghitung Jarak terdekat titik pada Kurva grafik
Misalkan:
M= (a,b)= (6,0)
Asumsikan ada satu titik pada kurva /grafik y=2$\sqrt x$ yakni (x,y).
$ MN= \sqrt {(x-a)^2 + (y-b)^2} \\ MN= \sqrt {(x-6)^2 + (y-0)^2}$
Subtitusikan y=2$\sqrt x$
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2} \\ MN = \sqrt { x^2-12x+36 +4x} \\ MN = ( x^2-12x+36 +4x)^ {\frac {1}{2}}$
Sesuai syarat maksimum dan minimum dimana terjadi saat turunan pertama =0 maka,
$ \frac {d(MN}{dx}=0 \\ \frac {2x-12+4}{ \sqrt { x^2-12x+36 +4x} } =0 \\ 2x-8 =0 \\ x=4$
Jadi jarak terdekat itu terjadi saat x=4. Silakan disubtitusi ke persamaan:
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2}\\ MN =\sqrt {(4-6)^2 + (2\sqrt 4-0)^2} = 2 \sqrt 5$.
Semoga pembahasan soal Contoh Soal Jarak Terdekat Titik ke Kurva dengan Turunan ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.
Cari Soal dan Pembahasan tentang turunan
Loading...