Contoh Soal Nilai Maksimum untuk Luas Persegi Panjang

Topik Bahasan turunan
Diketahui segitiga ABC dengan panjang AB = AC = 13 cm dan panjang BC = 10 cm. Di dalam segitiga tersebut akan dibuat sebuah persegi panjang. Luas maksimum persegi panjang yang terjadi adalah ....

A. 60 cm$^2$
B. 48 cm$^2$
C. 40 cm$^2$
D. 30 cm$^2$
E. 28 cm$^2$

Pembahasan:

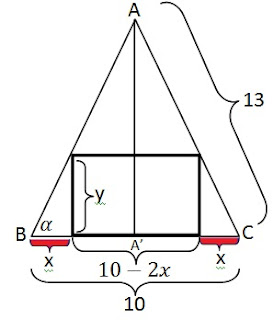
Pertama silakan dilukis segitiga yang dimaksud.

Misalkan lebar segitiga y. Lalu panjang bagian sisa segitiga kanan kiri x. Sehingga panjang persegi panjang menjad 10-2x.

Perhatikan segitiga ACA'. Karena sama kaki, maka siku siku di A'. Selanjutnya gunakan dalil Phytagoras. untuk menghitung AA'.

$ AA' = \sqrt {AC^2-A'C^2} = \sqrt {13^2-5^2} =12$

Selajutnya perhatikan segitiga ,

Segitiga MM'C dan AA'C sebangun. (sudut A = Sudut M, sudut C= sudut C dan Sudut M'= sudut A') su-su-su.

Bisa dibikin perbandingan sesuai kesebangunan:

$ \frac {MM'}{AA'} = \frac {CM'}{CA'} \\ \frac {y}{12}\frac {X}{5}\\ y= \frac {12x}{5}$

Sementara itu luas segiempat:

L = p.l

L =(2x-10).y

L=(2x-10).$\frac {12x}{5}$

L=$ \frac {24x^2}{5}-24x$

Nilai maksimum terjadi saat Turunan pertama sama dengan 0. Artinya L'=0.

L'= $\frac {48x}{5}$ - 24

0=$\frac {48x}{5}$ - 24

$x= \frac {5}{2}$

Perhatikan persamaan Luas;

L=$ \frac {24x^2}{5}-24x$, subtitusikan $x= \frac {5}{2}$

Sehingga

L= $ \frac {24( \frac {5}{2})^2}{5}-24. \frac {5}{2}$

L= 30 cm$^2$

Kunci Jawaban D

.

Semoga pembahasan soal Contoh Soal Nilai Maksimum untuk Luas Persegi Panjang ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.

Cari Soal dan Pembahasan tentang turunan