Topik Bahasan
geometri ruang
Untuk dasar menghitung jarak titik ke garis bisa dibaca di : Cara Menghitung Cara Titik ke Garis
Soal 1:
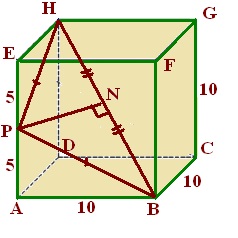
Diketahui titik P ada ditengah-tengah garis EA pada kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik P ke garis BH?
Penyelesaian:
Jarak P ke garis BH diwakili oleh garis PN karena PN tegak lurus dengan BH.
Menentukan panjang sisi-sisi segitiganya :
panjang PB = PH = $ \sqrt{PA^2 + PB^2} = \sqrt{5^2 + 100^2} = 5\sqrt{5} $
Karena segitiga PBH samakaki, maka letak N terletak ditengah BH.
Panjang $ BN = \frac{1}{2} BH = \frac{1}{2} \times 10\sqrt{2} = 5\sqrt{2} $
Menentukan panjang PN, menggunakan segitiga PBN
$ \begin{align} PN & = \sqrt{PB^2 - BN^2} \\ & = \sqrt{(5\sqrt{5})^2 - (5\sqrt{2})^2} \\ & = 5\sqrt{3} \end{align} $
Jadi, jarak P ke garis BH adalah $ 5\sqrt{3} \, $ cm.
Soal 2:
Tentukan jarak titik A ke garis EF pada kubus ABCD.EFGH yang memiliki panjang rusuk 10 cm?
Pembahasan:
Jika titik A kita proyeksi ke garis EF, maka hasilnya adalah titik E karena AE tegak lurus dengan EF. Sehingga jarak titik A ke garis EF adalah 10 cm..
Semoga pembahasan soal Soal-Jawab Jarak Titik ke Garis ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.
Untuk dasar menghitung jarak titik ke garis bisa dibaca di : Cara Menghitung Cara Titik ke Garis
Soal 1:
Diketahui titik P ada ditengah-tengah garis EA pada kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik P ke garis BH?
Penyelesaian:
Jarak P ke garis BH diwakili oleh garis PN karena PN tegak lurus dengan BH.
Menentukan panjang sisi-sisi segitiganya :
panjang PB = PH = $ \sqrt{PA^2 + PB^2} = \sqrt{5^2 + 100^2} = 5\sqrt{5} $
Karena segitiga PBH samakaki, maka letak N terletak ditengah BH.
Panjang $ BN = \frac{1}{2} BH = \frac{1}{2} \times 10\sqrt{2} = 5\sqrt{2} $
Menentukan panjang PN, menggunakan segitiga PBN
$ \begin{align} PN & = \sqrt{PB^2 - BN^2} \\ & = \sqrt{(5\sqrt{5})^2 - (5\sqrt{2})^2} \\ & = 5\sqrt{3} \end{align} $
Jadi, jarak P ke garis BH adalah $ 5\sqrt{3} \, $ cm.
Soal 2:
Tentukan jarak titik A ke garis EF pada kubus ABCD.EFGH yang memiliki panjang rusuk 10 cm?
Pembahasan:
Jika titik A kita proyeksi ke garis EF, maka hasilnya adalah titik E karena AE tegak lurus dengan EF. Sehingga jarak titik A ke garis EF adalah 10 cm..
Semoga pembahasan soal Soal-Jawab Jarak Titik ke Garis ini bermanfaat untuk anda. Jika ada pertanyaan atau soal yang ingin di bahas bisa pilih menu tanya soal. Terima kasih dan sampai jumpa di masalah masalah berikutnya guys.
Cari Soal dan Pembahasan tentang geometri ruang
Loading...